Définition d’un triangle rectangle
Un triangle rectangle, comme son nom l’indique, est un type particulier de triangle qui a la caractéristique d’avoir un angle de 90 degrés, donc un angle droit. Un attribut très spécifique et qui permet de distinguer instantanément ce type de triangle des autres. Il a une allure un peu particulière, semble toujours un peu plus solide, plus stable.
Compréhension du terme ‘hypoténuse’
Alors, faisons une première rencontre avec ce terme un peu étrange : l’hypoténuse. C’est le côté le plus long d’un triangle rectangle. Il est toujours situé en face de l’angle droit. En somme, c’est un côté très particulier qui, nous le verrons, détient une place importante dans certaines théories mathématiques.
Rappel de l’importance des mathématiques
Rappelons-nous avant tout que les mathématiques sont une science essentielle qui ont permis à l’humanité de comprendre et de décrire le monde qui nous entoure de façon logique et précise. Ce sont très souvent les mathématiques qui se cachent derrière les grandes prouesses technologiques et scientifiques de notre époque.
Le Théorème de Pythagore
Présentation du Théorème
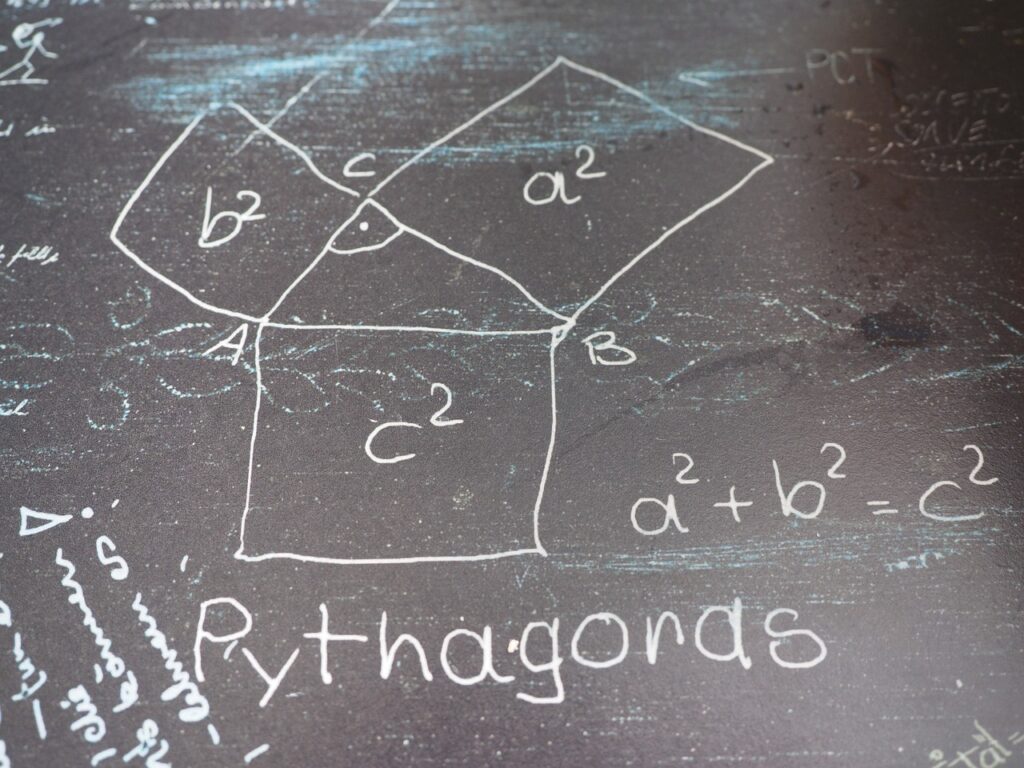
Un vieux grec du nom de Pythagore, qui était en fait bien plus qu’un simple grec, il était aussi un grand philosophe et théoricien de son époque, a énoncé une théorie célèbre que l’on appelle aujourd’hui ‘le Théorème de Pythagore’. Cette théorie dit que : « le carré de l’hypoténuse est égal à la somme des carrés des deux autres côtés. »
Démonstration du Théorème
Maintenant, faisons une petite démonstration du théorème de Pythagore pour mieux nous approprier cette théorie. Imaginons donc que j’ai un triangle rectangle devant moi. Selon Pythagore, si je prends la longueur du côté A, que je la mets au carré, que je fais la même chose pour la longueur du côté B et que j’additionne les deux, cela me donnera la longueur de l’hypoténuse (C) au carré. Ainsi, l’équation de ce théorème devient: A² + B² = C². C’est aussi simple que ça!
Importance du Théorème de Pythagore dans le calcul de l’hypoténuse
Vous vous demandez peut-être pourquoi cette théorie est si importante ? Eh bien, elle va nous donner le moyen de calculer la longueur de l’hypoténuse, le fameux côté le plus long du triangle rectangle, en se basant sur la longueur des deux autres côtés. Une découverte qui a permis d’avancer en trigonométrie et en mathématiques en général.
Preuve de la pertinence du Théorème de Pythagore
La preuve de la pertinence du théorème de Pythagore est simple : il a survécu à l’épreuve du temps. Depuis son énonciation par Pythagore, qui a vécu vers le VIe siècle av.J-C, jusqu’à nos jours, cette théorie n’a pas été réfutée. Elle est au contraire largement adoptée dans le monde de la géométrie et des mathématiques et est enseignée dans les écoles du monde entier.
Calculer l’hypoténuse dans un triangle rectangle
Comment identifier les côtés d’un triangle rectangle
Dans un triangle rectangle, l’hypoténuse est donc le côté le plus long et toujours positionné en face de l’angle droit. Les deux autres côtés, ceux qui forment l’angle droit, sont appelés « côtés adjacents ».
Méthodologie pour calculer l’hypoténuse
Pour calculer la longueur de l’hypoténuse dans un triangle rectangle, on utilise la formule fournie par le Théorème de Pythagore. Ainsi, si nous connaissons les longueurs des deux côtés adjacents, nous pouvons aisément trouver la longueur de l’hypoténuse.
Des exemples de calcul de l’hypoténuse
Par exemple, imaginons que nous avons un triangle rectangle avec des côtés de 3 cm et 4 cm. En utilisant le Théorème de Pythagore, nous pouvons calculer que l’hypoténuse serait de √(3² + 4²) = 5 cm. Un calcul simple mais qui nous permet d’avancer efficacement dans la résolution de problèmes géométriques plus complexes.
L’étape essentielle de la vérification
Comme toujours en mathématiques, une fois le calcul de l’hypoténuse réalisé, il est important de vérifier l’exactitude de son résultat. Pour cela, on pourra par exemple dessiner le triangle et vérifier que l’hypoténuse obtenue par le calcul est bien le côté le plus long, ou encore vérifier que la formule du théorème de Pythagore est respectée avec les longueurs calculées.
Applications de l’hypoténuse
Utilisation de l’hypoténuse dans différents domaines
L’hypoténuse, une fois qu’on sait comment la calculer, se retrouve partout. En effet, elle est utilisée dans de nombreuses disciplines comme l’architecture, la topographie, la navigation, la physique, etc. Elle est une véritable clé pour calculer des distances, des angles, des vitesses, et bien plus encore.
Lien entre l’hypoténuse et la trigonométrie
D’autre part, la trigonométrie, qui est une branche des mathématiques qui étudie les relations entre les longueurs des côtés des triangles rectangles et les angles de ces triangles, utilise l’hypoténuse à chaque instant. Sans l’hypoténuse, impossible de faire du sinus, du cosinus ou du tangente. L’hypoténuse est donc un élément central de la trigonométrie.
Conclusion
Vu sous cet angle, calculer l’hypoténuse d’un triangle rectangle est une compétence accessible et qui a de nombreuses applications pratiques. Et surtout, on a vu au cours de ce guide que le calcul de l’hypoténuse d’un triangle rectangle est facile grâce au Théorème de Pythagore.
Calculer l’hypoténuse d’un triangle rectangle va bien au-delà de la simple résolution d’un problème de mathématiques. En réalité, c’est un excellent exercice pour renforcer ses compétences en résolution de problèmes et en pensée spatiale, deux compétences essentielles en mathématiques et en sciences en général.
Je conclurais en vous rappelant que, comme pour toute compétence, la pratique est la clé! Plus vous pratiquerez, plus le calcul de l’hypoténuse deviendra une seconde nature pour vous. A vous de jouer !
A bientôt pour plus de leçons claires et détaillées de mathématiques!